Hello Everyone!💚

This article is everything you need to know about array rotation. Array Rotation is one of the most important concepts, used in a wide range of problems which includes shifting of elements.

CONTENTS

1. What is array rotation?
2. Some of the approaches...
3. Understanding juggling algorithm
4. Hands-on coding for left rotation
5. An easy method for the right rotation

What is array rotation?

By name, we can understand that rotation means simply shifting elements of an array by a specified number of positions. Rotations can be of 2 types: left and right. See below examples to get a clear understanding of what it is.

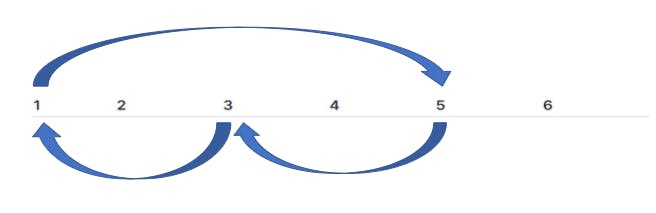
Left Rotation: Here, k=2 (where k is the number of positions to be shifted left).

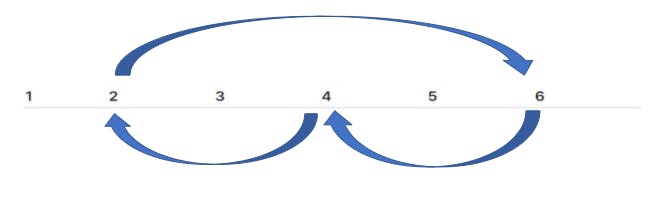
Right Rotation: Here, k=2 (where k is the number of positions to be shifted right).

Did you spot the difference between these two examples? Great! Let's proceed further.😁

Some of the approaches...

1. By using a temporary array

   arr[]=[1,2,3,4,5], k=2
   1.) storing the elements to be rotated in temp[]
   temp[]=[1,2]  //considering left shift
   2.) shifting elements to left in arr[]
   arr[]=[3,4,5,4,5]
   3.)Storing back the elements in temp[]
   arr[]=[3,4,5,1,2]
   

2. By rotating elements one by one

   arr[]=[1,2,3,4], k=2
   //left rotate
   1.) [2,3,4,1]
   2.) [3,4,1,2]
   

   Other methods include block-swap algorithm, reversal algorithm, juggling algorithm, etc. We know, one code can be written in many ways. But, choosing an optimal code is the ultimate goal.

   

Understanding juggling algorithm

• Consider an array of length n=6, k=3 (assume).

1	2	3	4	5	6

• Consider the greatest common divisor of n,k as g. Divide the array into g sets. Therefore, here g=3 so, sets are {1,2},{3,4},{5,6}.
• Now, rotate the first elements in all sets to left and later followed by the next element rotations till the last element in set gets rotated.

  

3	2	5	4	1	6

3	4	5	6	1	2

After all rotations, we have obtained the final required array.Now, we are aware of the concept. Let's try to code.😎

Hands-on coding for left rotation

1. writing a method gcd(n,k) to get gcd.

   int  gcd(int n,int k){
        if(n==0){
            return k;
        }
        if(k==0){
            return n;
        }
        if(n>k){
            return gcd(n-k,k);
        }
        else{
            return gcd(n,k-n);
        }
    }
   

2. After obtaining gcd, we have to write code for shifting corresponding elements in each block.

void juggle(int[] arr,int n,int k){
        int g=gcd(n,k);
        int temp,m,j;
        for(int i=0;i<g;i++){
          temp=arr[i];
          j=i;
          while(true){  //true
           m=j+k;
           if(m>=n){
               m=m-n;
           }
           if(m==i){
               break;
           }
           arr[j]=arr[m];
           j=m;
          }
         arr[j]=temp;  
        }
    }

After all the elements in the blocks(sets) are shifted, the array will be rotated in a way, which satisfies the required output.

Time Complexity: O(N) Space Complexity: O(1)

An easy method for right rotation

Let us consider the previous example,

1	2	3	4	5	6

Left Rotation(k=2)

3	4	5	6	1	2

Right Rotation(k=2)

5	6	1	2	3	4

Left Rotation(k=4)

5	6	1	2	3	4

Here, to write a code for right rotation just observe the examples carefully. If you see, we can get the output of the right rotation by considering k=4 for left rotation. Therefore, for right rotation just consider k=n-k.

That's it! You have learnt how to juggle arrays😍